Adam Pavlůsek (2006) - Bakalářská práce

Výsledky

Tato kapitola bakalářské práce je členěna podle morfometrických charakteristik, kterou zkoumáme. Součástí hodnocení jsou mapové výstupy, tabulky a grafy.

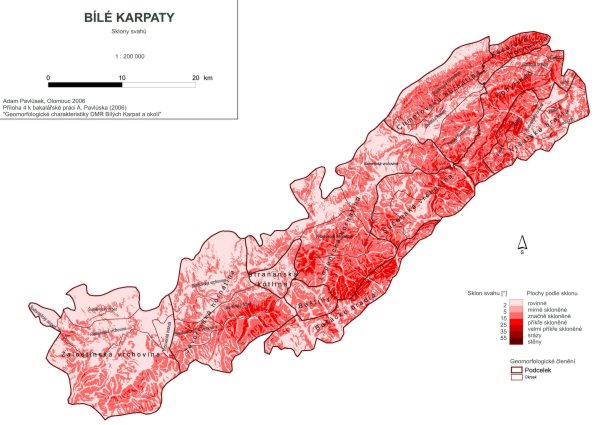
Sklony svahů

Sklony svahů představují jednu ze základních morfometrických charakteristik reliéfu. V prostředí GIS se jedná o fokální funkci, jež počítá hodnotu sklonu svahu pro každý pixel gridu z hodnot nadmořských výšek nejbližších buněk.

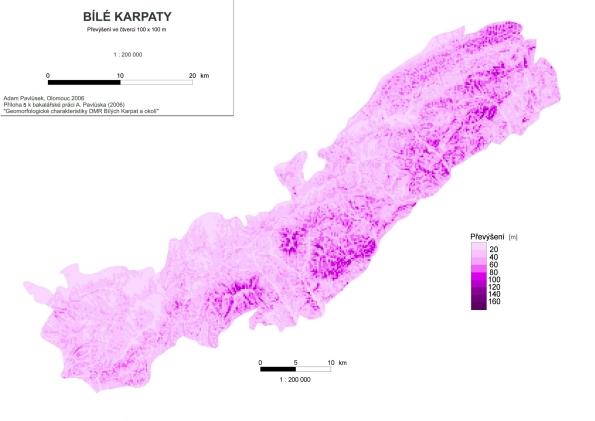
Převýšení

Veličina převýšení udává absolutní hodnotu rozdílu nadmořských výšek, tedy rozdíl mezi nejvyšší a nejnižší hodnotou nadmořské výšky v dané filtrovací jednotce. Tato charakteristika nám podá informaci o výškových poměrech v terénu a jednou ze základních charakteristik pro zkoumání výškové členitosti území. Pro zjištění jeho hodnot z gridu byl využit blokový filtr o rozměru 4 x 4 buňky, což odpovídá rozměru 100 x 100 m.

Křivost reliéfu

Každý povrch má obecně různé křivosti v různých směrech. Pro použití v geovědách je důležitá křivost ve směru gradientu (profilová křivost), protože vyjadřuje změnu úhlu sklonu georeliéfu, čímž je vyjádřena změna rychlosti toku hmoty podél spádnicové křivky. Křivost kolmá na gradient (planární křivost) vyjadřuje změnu velikosti úhlu orientace svahů, což ovlivňuje divergenci a konvergenci vodních toků. Obě křivosti se měří v normálových rovinách.

Kladné a záporné hodnoty profilové a planární křivosti mohou být kombinovány k definování elementárních forem georeliéfu. Každá elementární forma má rozdílný tok materiálu. Konvexní a konkávní formy ve směru gradientu mají tok urychlený a zpomalený, a konvexní a konkávní formy ve směru tečny k vrstevnici mají tok konvergentní a divergentní.

Planární křivost

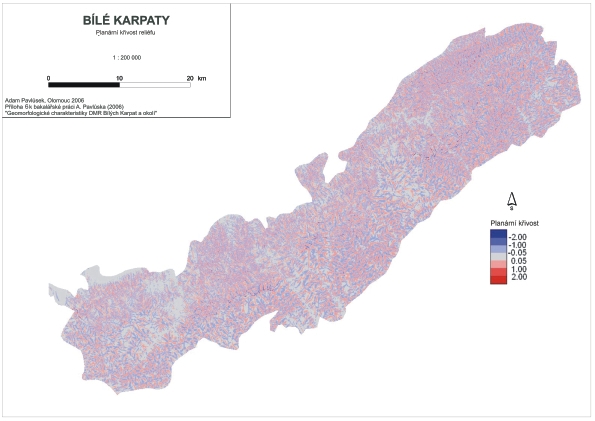
Profilová křivost

Orientace plošných prvků a konečných částí povrchu

Vedle tvaru terénních prvků a částí terénu může být důležitým kritériem při členěním zemského povrchu také jejich orientace ke světovým stranám, neboť společně se sklonem terénu je hlavní složkou tzv. expozice. Jestliže tvar terénních prvků a jejich uspořádání v terénní ploše určují další vývoj tvarů povrchu, mají dohromady s expozicí komplexnější vliv na charakter krajiny, zejména pokud jde o uspořádání povrchových vod a jejich odtok, o porosty atd.
Orientace plošných prvků je dána azimutem alfa průmětů spádových křivek ve středech těchto prvků. Čáry stejné orientace topografické plochy lze vyhledat na jejím vrstevnicovém obrazu jako spojnice dotykových bodů rovnoběžných tečen vedených k vrstevnicím. Tyto tečny jsou vodorovnými povrchovými přímkami obecných válcových ploch obalujících topografickou plochu a dotykové čáry proložené zmíněnými dotykovými body jsou hranicí mezi plošnými částmi s orientací stočenou v kladném nebo záporném směru až po stejně nebo jinak orientovanou hraniční čáru (Kudrnovská, 1965).

Horizontální členitost v souvislosti se soustavou vodních toků

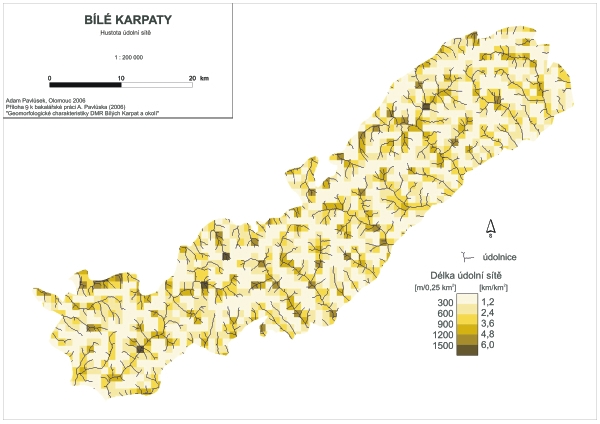
Topografická plocha s vyvinutými údolními a rozvodními čarami má nejen svoji vertikální členitost, ale i horizontální, závislou hlavně na struktuře a hustotě údolní sítě. Čím větší je v krajině hustota vodních toků, tím složitější je průběh horizontálních křivek a z nich vybraných vrstevnic.

HVS (hustota vodní soustavy) nemůže být posuzována jen podle délek vodních toků zakreslených na mapě, poněvadž nikdy nemáme spolehlivou informaci o tom, který stav je v mapě zachycen, tj. zda je to situace za suchých, průměrných nebo extrémních srážkových období, což by mapové obrazy vodních toků různě zkracovalo nebo prodlužovalo. Na stavu výchozí mapy a na stupni výběru by pak byla závislá nejen délka vodních toků, ale i na její jednotku připadající plocha povodí (km/km2), nebo naopak délka vodních toků připadající na jednotku plošnou (km2/km), čili HVS.

Hustota vodní soustavy nemůže proto, pro závislost na definici vodního toku, použité při kresbě topografického obsahu mapy, být kritériem pro posuzování horizontální členitosti reliéfu. Východiska z této situace se nabízejí dvě: buď místo HVS (vypočítané z délek v mapě zakreslených vodních toků) zavedeme hustotu údolní sítě či soustavy, nebo vodním tokům přiřkneme různé váhy. Ani tato východiska nejsou bez problémů. V prvním případě je to definice údolí a jeho počátku, třebaže není tak neurčitá, jako definice počátku vodního toku. Odpověď na otázku lze zjednodušit, uvažujeme-li jen o stálých a zřejmých povrchových tocích, a o údolích, jakožto rezultátu denudačních a erozních procesů. Údolí v těchto reliéfech, které jsme označili jako „říčně erozní“, není obtížné vyhledat podle toho, co bylo na začátku řečeno o členění reliéfu. Neexistují jiné začátky údolí nežli ty, které leží v sedlech nebo na tzv. čarách parabolických bodů, a pak již není taková nejistota při uzavírání „buněk“ nebo „ok“ sítě. Hustotu údolní sítě lze určovat mnohem přesněji než hustotu vodních toků a také je to charakteristika, která je použitelnější při úvahách o výškové členitosti nežli HVS.

Izobazity

Izobazity tvoří povrch, který je interpolován mezi hodnotami nadmořských výšek jednotlivých údolnic. Vzniká tak povrch, jehož tvar vypovídá o rozdílech zařezání jednotlivých údolí do podloží. Nepravidelnosti takového tvaru napovídají o anomáliích v rozložení podkladových hornin nebo úklonu vrstev.

Pro tuto analýzu mi poslouží grid údolní sítě, vytvořený u zkoumání hustoty údolní sítě. Tento grid byl vynásoben gridem nadmořských výšek, abychom dostali hodnotu nadmořské výšky pro každý pixel údolní sítě. Tyto body spolu poté interpolujeme, abychom dostali nový povrch, který reprezentuje izobazity.

Spádový index (SL-index)

Pro každý úsek toku lze stanovit tzv. spádový index (SL-index) pomocí kterého lze srovnávat gradient toků různé velikosti. Tento index podle něj odráží energii toku (schopnost toku konat práci) a jednoduchým způsobem kombinuje dva morfometrické parametry spádové křivky: spád toku v daném úseku a vzdálenost středu tohoto úseku od pramene (měřeno po proudu nejdelšího toku). V rámci jakéhokoliv uspořádání reliéfu tak hodnoty SL-indexu závisí na celkovém převýšení povodí a režimu toku. Při interpretaci změn hodnot SL-indexu podél toku je tedy nezbytné komplexně uvažovat proměnné jako je proměnlivost v litologii podloží, množství materiálu dodávaného do toku, klimatické a tektonické eventy a geomorfologickou historii území, přičemž litologické a tektonické faktory se zdají mít na průběh hodnot spádového indexu největší dopad.

Rovnice pro sklon (spád) může být vyjádřena v následujícím tvaru:

SL=k

Protože hodnota k vyjadřuje sklon logaritmického profilu pro daný segment, lze ji použít jako index relativního sklonu reálné spádové křivky v daném bodě. Výsledek vztahu SL (který je ekvivalentem konstanty k v rovnici), se nazývá spádový index (SL-index).

SL-index je významnou charakteristikou, protože zhruba vyjadřuje kompetenci (energii toku) toků transportovat materiál o určité velikosti a má vztah i k charakteristikám vyjadřujícím odpor řečiště vůči proudění. Tyto závěry byly potvrzeny i empiricky, jak ukazuje Hackova (1957) studie zabývající se vodními toky v povodí řeky Potomac (USA), kde byly nalezeny významné souvislosti mezi velikostí dnového materiálu, délkou toku a spádem (podle Bíl, Máčka 1999).

Strahlerův hypsometrický integrál (SHI)

Strahlerův hypsometrický integrál (SHI) vyjadřuje poměr mezi objemem hmoty v současném a v původním reliéfu (poměr mezi erodovaným a kompletním reliéfem) v daném území. Hodnota SHI je tedy nepřímo úměrná množství odneseného materiálu z daného území, přeneseně tedy vyjadřuje stáří daného reliéfu (čím menší hodnota SHI, tím více odneseného materiálu, tím je území starší). Jedná se tedy o veličinu, jež teoreticky nabývá hodnoty v rozmezí 0 až 1, resp. 0 – 100%.

Hodnotu SHI je možno znázornit hypsometrickou křivkou, která zjednodušeně kopíruje profil daného území. Vychází z relativní nadmořské výšky a plochy území. Velikost plochy pod křivkou pak odpovídá hodnotě SHI. Podle tvaru hypsometrické křivky můžeme dále posoudit svažitost daného území, proto je zřejmé, že pro území se stejným geomorfologickým vývojem bude nejstrmější křivka bude vycházet pro povodí nejvýše položená (Strahler, 1952).