Stanovení minimální absolutní chyby při procesu tvorby DMR
s využitím statistického porovnání v prostředí softwaru R

Digitální modely reliéfu jsou prvním krokem k odvozeným parametrům, které slouží množství geografických aplikací. Moore et al. (1991) je rozdělují na primární topografické atributy, které se odvozují přímo z DMR, a sekundární atributy, jež kombinují primární atributy s fyzikálními či empirickými indexy. Mnoho prací dokázalo, že chyba v původním DMR může způsobit větší chyby v odvozených površích (viz např. Oksanen, Sarjakoski, 2005 nebo Wilson, Gallant, 2000). Proto je kladen takový důraz na přesnost modelů reliéfu.

V dnešní době již máme technologie, které poskytují rovnou rastrovou informaci o nadmořské výšce. Stále však potřebujeme interpolační metody, které z diskrétních vstupních dat zajistí odhad hodnot pro neznámá místa.

Kvalitu interpolace lze posoudit např. tzv. bumerangovým testem, kdy se na části známých hodnot provede interpolace a vzniklý povrch se porovná se známými hodnotami bodů, které byly z interpolace vynechány. Metodu je vhodné opakovat pro různé výběry ze sady známých bodů.

Běžně smýšlíme o interpolaci: tedy o metodě, která poskytuje informaci o hodnotě jevu mezi známými hodnotami. Je třeba si však uvědomit, že ne všechny metody zvládají hodnoty extrapolovat za hranici území určenou krajními body (např. lineární triangulace).

Interpolační metody lze různě klasifikovat… Předně je to rozdělení na metody exaktní a aproximující. Exaktní metody zachovávají naměřené hodnoty, tzn. že výsledný povrch přesně prochází vstupními body. Aproximující metody naproti tomu nectí původní hodnoty a ve výsledném povrchu se v jejich místech může objevit hodnota jiná.

Lokální interpolace využívá k odvození neznámých hodnot omezený počet známých bodů v okolí. Zatímco metody globálního odhadu analyzují celou sadu známých hodnot, tzn. že změna jediné vstupní hodnoty má vliv na výsledné hodnoty na celém území. Existují i metody kombinující oba přístupy – např. když regresní modely stanoví globální statistiku a pak ji lokálně zjemní blízkými hodnotami (Hartkamp et al., 1999). Ovšem lokální metodě lze nastavit takové parametry (vyhledávací poloměr), že se bude chovat jako globální.

Stochastická (geostatistická) je metoda, která uvažuje náhodnost a statistický vztah mezi všemi vstupními hodnotami (např. kriging, regresní modely). Výsledný povrch je vnímán jako jeden z mnoha, který mohl být na základě vstupních bodů sestaven. Stochastické procedury umožňují stanovit statistickou významnost povrchu (přesnost) a neurčitost výstupních hodnot. Deterministické metody naopak nepracují s pravděpodobností a jejich výsledek je ryze matematicky určen. (Goodchild, Kemp, 1990, ArcGIS Desktop Help)

Dále rozlišujeme, zda metoda generuje spojitý (continuous, gradual) či nespojitý (diskrétní, broken, abrupt) povrch. Opět zde platí, že variantním nastavením parametrů vybraných metod lze dospět k oběma typům povrchů. Spojitost může také ovlivnit použití bariér. Ty mohou být buď polopropustné, které generují spojitou rychlou změnu hodnot (atmosférické fronty), nebo nepropustné, které produkují ryze nespojitý povrch (geologické zlomy) (Goodchild, Kemp, 1990).

Podle Schejbala (1996) poskytuje geostatistická teorie velmi účinný aparát pro studium a modelování přírodních objektů a jevů, protože umožňuje postihnout jak náhodný, tak nenáhodný (strukturální) charakter prostorové distribuce veličin. Geostatistická strukturální analýza je totiž schopna popsat kontinuitu, homogenitu, stacionaritu a izotropii hodnot v území. Základním nástrojem je analýza semivariogramu, vektorové strukturální funkce vyjadřující závislost průměrné kvadratické diference známých hodnot na jejich vzdálenosti. Kontinuita je pak vyjádřena dosahem semivariogramu – je tak odhalen vyhledávací poloměr pro interpolaci v území. Za tímto dosahem už není třeba uvažovat vzájemné ovlivnění hodnot (nulová autokorelace). Při zjištění anizotropie pomocí směrových semivariogramů je pak možné zdeformovat kruhový vyhledávací poloměr a definovat různý dosah v různých směrech.

Triangulace je obecně založena na překrytí známých bodů systémem trojúhelníků. Z nepravidelně rozmístěného bodového pole lze vytvořit mnoho různých trojúhelníkových sítí. Optimalizačním kritériem může být např. co největší rovnostrannost trojúhelníků, jejich minimální obvod apod. (Tuček, 1998) Nejčastěji je však implementována tzv. Delaunay triangulace, která vyžaduje, aby v kružnicích opsaných trojúhelníkům nebyl žádný další bod. Dualitou k Delaunay triangulaci jsou tzv. Thiessenovy polygony (Voronoi teselace).

Vrcholy trojúhelníků představují známé hodnoty (jedná se o exaktní metodu). Spojnice dvou bodů jsou místa styku dvou trojúhelníků – v těchto místech dochází ke skokové změně sklonu a orientace trojúhelníkových plošek. Ač je tedy takový povrch spojitý, jeho další derivace nejsou. Trojúhelníková ploška je rovinou definovanou trojicí bodů. Lokální odhad neznámé hodnoty se vypočítá lineární interpolací hodnot bodů ve vrcholech trojúhelníka, do kterého místo odhadu přísluší. Jedná se o deterministickou metodu.

Metoda podává lepší výsledky, pokud je aplikována na hustší datové pole. Podle průměrné velikosti trojúhelníků pak lze usuzovat na optimální velikost rastrové buňky pro minimalizaci chyb způsobených neregulérností vyšší derivací povrchu.

Lineární triangulace povrchu z vrstevnicového modelu trpí nedostatečnou hustotou vrstevnic a jejich konfigurací. Nezřídka se v neošetřených TINech vyskytují plochá místa tam, kde jednotlivé trojúhelníky tvoří body stejné vrstevnice. Tento fenomén se obvykle odstraňuje vložením tzv. VIP bodů do „ohrožených“ oblastí (vrcholy, údolí).

Tato metoda bývá často přibližována Toblerovým tzv. prvním zákonem geografie. Metoda inverzních vzdáleností (Inverse Distance Weighted) je deterministickou metodou – využívá váženého lineárního průměru nejbližších bodů. Vahou je vzdálenost umocněná zvoleným parametrem power. Vyšší hodnota tohoto parametru přisuzuje větší vliv bližším bodům, a generuje tak členitější povrch s charakteristickými koncentrickými izoliniemi. Nižší hodnota pak vytváří hladší povrchy, šanci promluvit do hodnoty interpolovaného bodu dostávají i vzdálenější body. Hodnota nula však IDW degraduje na prostý průměr vybraných hodnot bez vážení vzdáleností. Nejčastěji se používá druhá mocnina vzdálenosti – pak mluvíme o Inverse Distance Square, doporučené hodnoty jsou 1–3.

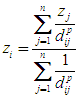
z_i … interpolovaná hodnota;
z_j … známá hodnota;
n … počet vybraných známých bodů v okolí;
p … power;
d_ij … vzdálenost z_i a z_j.

IDW je primárně exaktní metodou. Byly však sestaveny varianty IDW, které zahrnují vyhlazovací faktor ke zmírnění tendence nadhodnocování blízkých bodů. Jedná se např. o Shepardovu metodu, která ke shlazení používá metodu nejmenších čtverců (Surfer Help).

IDW je lokální metodou. Druhý parametr specifikuje, kolik známých bodů v okolí bude vybráno pro interpolaci hodnoty neznámého bodu. Běžně se používá buď určitý počet nejbližších sousedů (Nearest Neighbors), nebo specifický vyhledávací poloměr (Fixed Radius). Systém Surfer umožňuje např. i výběr z oktantů či směrové vážení (Directional weighting). Při výběru z oktantů je vybrán jeden nejbližší bod z každé 45-stupňové výseče okolo interpolovaného místa. Při směrovém vážení je vyhledávací okruh rozdělen na výseče definovaných úhlů a váhami jsou zvýhodněny výseče v určitém směru – body z těchto výsečí pak mají větší vliv než stejně vzdálené body v jiných výsečích.

V extrémním případě může být vybrán jediný nejbližší bod, jedná se pak o nespojité Thiessenovy polygony. Bod se známou hodnotou leží uprostřed takového polygonu – vymezuje tak sféru svého výlučného vlivu. Každý bod uvnitř polygonu má blíže k centrálnímu známému bodu svého polygonu než ke kterémukoli jinému známému bodu.

Spline je metodou minimální křivosti – základním požadavkem na výsledný povrch je minimalizace druhé derivace povrchu. Jedná se o lokální a exaktní metodu. Polynomické křivky (deterministická metoda) přesně procházejí vybranými body a je důležité, aby byla zajištěna spojitost na jejich styku. Výsledkem je hladký povrch, ale také falešná maxima a minima. Deprese v DMR jsou přitom podle Riegera (1998) hlavním problémem v hydrologických aplikacích.

Spline je exaktní metoda, avšak i ta má svou aproximující variantu. Implementace metody minimální křivosti v systému Surfer umožňuje nastavit parametr Maximum Residual jako maximální chybu proti známých hodnotám. Nasazení povrchu se pak děje iteracemi, dokud není dosažena nastavená hodnota. Lam (1983) uvádí mezi aproximujícími metodami i metodu nejmenších čtverců pro Spline.

Produkty ESRI nabízejí dvě základní varianty metody, a to regularizovaný spline a spline s tenzí. Regularizovaný spline obvykle poskytuje hladší povrchy než tenze. Kromě počtu bodů (minimum je 8) se nastavuje parametr weight. U regularizovaného definuje váhu třetích derivací povrchu ve výrazu minimalizace křivosti. Vyšší váha generuje hladší výsledný povrch. ESRI doporučuje hodnoty: 0, 0.001, 0.01, 0.1 a 0.5.

Weight pro spline s tenzí kontroluje váhu pnutí, tuhosti povrchu. Vyšší hodnota způsobuje větší drsnost povrchu. Doporučenými hodnota jsou 0, 1, 5 a 10, nicméně nastavení váhy na nulu podle Kadlčíkové a Tučka (2008) generuje velmi vysokou RMSE chybu v porovnání s ostatními nastaveními parametru.

Mitášová a Mitáš (1993) prezentují spojenou metodu, regularizovaný spline s tenzí. Kromě toho odkazují na vývoj metody Spline od roku 1974 i na globální variantu metody.

Kriging je založen na strukturální analýze studovaného území (viz Schejbal, 1996). Jedná se o širokou geostatistickou (stochastickou) metodu, kterou lze použít jak k odhadu lokálnímu (s globálním variogramem či trendem), tak ke globálnímu. U krigování se objevuje i pojem blokový odhad.

Ve své základní podobě kriging počítá novou hodnotu jako váženou lineární kombinaci známých hodnot v definovaném okolí bodu. Váhy jsou pro každý neznámý bod sestaveny podle vzdálenosti, hodnoty semivariogramu a podle principu minimalizace výsledného rozptylu řešením soustavy lineárních rovnic.

Metoda zachovává naměřené údaje. Program Surfer však opět nabízí metodu i s vyhlazovacím faktorem.

Krigování se často zjednodušuje předpokladem lineárního modelu strukturální funkce, a to zvláště v případech, kdy počet známých hodnot není dostatečný na to, aby dokázal spolehlivě vykreslit tvar semivariogramu.

Produkty ESRI nabízejí dvě hlavní varianty metody: základní a univerzální. Základní předpokládá, že průměrná hodnota i prostorová autokorelace je v poli (kvazi-)konstantní. Univerzální naproti tomu uvažuje určitý trend, kterým lze popsat změnu průměrné hodnoty v poli.

Pro podrobnější popis podmínek, možností a variantních řešení metody doporučuji Schejbala (1996); základní použití se lze dozvědět i v ArcGIS Desktop Help.

Aproximuje povrch pomocí polynomických rovnic, přičemž nectí naměřené hodnoty a používá princip nejmenších čtverců. Jedná se o globální a deterministickou metodu, která se používá především pro zjišťování celkového trendu povrchu. V produktech ESRI lze pro řád polynomu použít hodnoty 1–12, typické hodnoty jsou 1–3. Polynom 1. řádu vytváří rovinný povrch. S každým vyšším řádem se výsledný povrch stává komplexnější, nelze však obecně říci, že přesnější. Přesnost lze odhalit pomocí RMSE a zvolit tak ideální řád polynomu pro konkrétní datovou sadu. V ArcGIS 9.3 je výpočet RMSE volitelným parametrem metody. (ArcGIS Desktop Help)