Použité metody a data
Použité metody
Úvodním krokem řešení práce bylo provedení literární rešerše za účelem hlubšího porozumění nesmírně široké problematiky v oblasti hodnocení kriminality. Další krok spočíval v nalezení vhodného zdroje veřejně dostupných prostorových dat o kriminalitě
za požadované období s největší možnou prostorovou podrobností v kontextu Česka.
V praktickém řešení naplnění cílů práce byla aplikována celá řada metod. Za účelem prostorové analýzy kriminality proběhlo seznámení se s daty a následovalo zpracování prostorových bodových dat kriminality mj. agregací dat na úrovni obcí, což vedlo k výpočtům souhrnných indexů kriminality v obcích Česka za roky 2016 až 2021. Mezi vypočtené souhrnné indexy kriminality náleží hrubý index kriminality a čistý index kriminality. V této praktické části práce bylo snahou vytvořit inovativní výpočet váženého indexu kriminality na základě přiřazení patřičných vah trestným činům podle průměrné doby odnětí svobody (nepodmíněného trestu) za sledovaný rok 2021. Pozornost byla věnována i analýze dílčích kategorií trestných činů.
Další významnou částí práce bylo posouzení vztahu kriminality k vybraným socioekonomickým ukazatelům. Pro tento účel byly použity metody prostorové statistiky, jako jsou regresní modely – Ordinary Least Squares (OLS) a jejich prostorové varianty – Spatial Lag Model (SLM), Spatial Error Models či geograficky vážené regrese (Geographically Weighted Regression – GWR). Charakteristika modelů je stručně popsána v závěru této podkapitoly.
Volba demografických a ekonomických ukazatelů byla uskutečněna v závislosti
na dostupnosti a aktuálnosti statistických dat požadované prostorové úrovně. Dalším kritériem pro volbu konkrétních statistických ukazatelů byla zmínka jejich přítomnosti
v některých ze zkoumaných studií a autorovým subjektivním posouzením vhodnosti
s ohledem na výsledky explorační analýzy vstupních dat.
Závěrečná část práce syntetizuje získané poznatky nalezení prostorových vztahů kriminality především z výsledků aplikace prostorových statistických modelů. Syntézou výsledků prostorových analýz je hodnocení kriminality ve vztahu k vybraným socioekonomickým ukazatelům. Dílčí výsledky hodnocení kriminality (tj. souhrnné indexy kriminality, jednotlivé kategorie trestných činů, nalezení prostorových vztahů vzhledem k vybraným socioekonomickým ukazatelům) byly zachyceny vhodnou prostorovou vizualizací sérií několika map užitím metody pseudokartogramu umožňující kvantitativní srovnávání jednotlivých dílčích územních celků, neboť forma geovizualizace ve srovnání s číselnými hodnotami, tabulkami
či grafy, dokáže přehledně zobrazit požadovanou prostorovou variabilitu vztahu.
Výstupy ve formě tabulek a grafů jsou rovněž zahrnuty jako součást diplomové práce.
V důsledku náročnosti funkcionality prostorových statistických modelů
je interpretace jejich výsledků a koeficientů značně obtížná. Z tohoto důvodu autor této diplomové práce přistupoval k interpretaci výsledků hodnocení kriminality s maximální možnou obezřetností. Grafická vizualizace postupu zpracování
je patrná z následujícího obrázku:
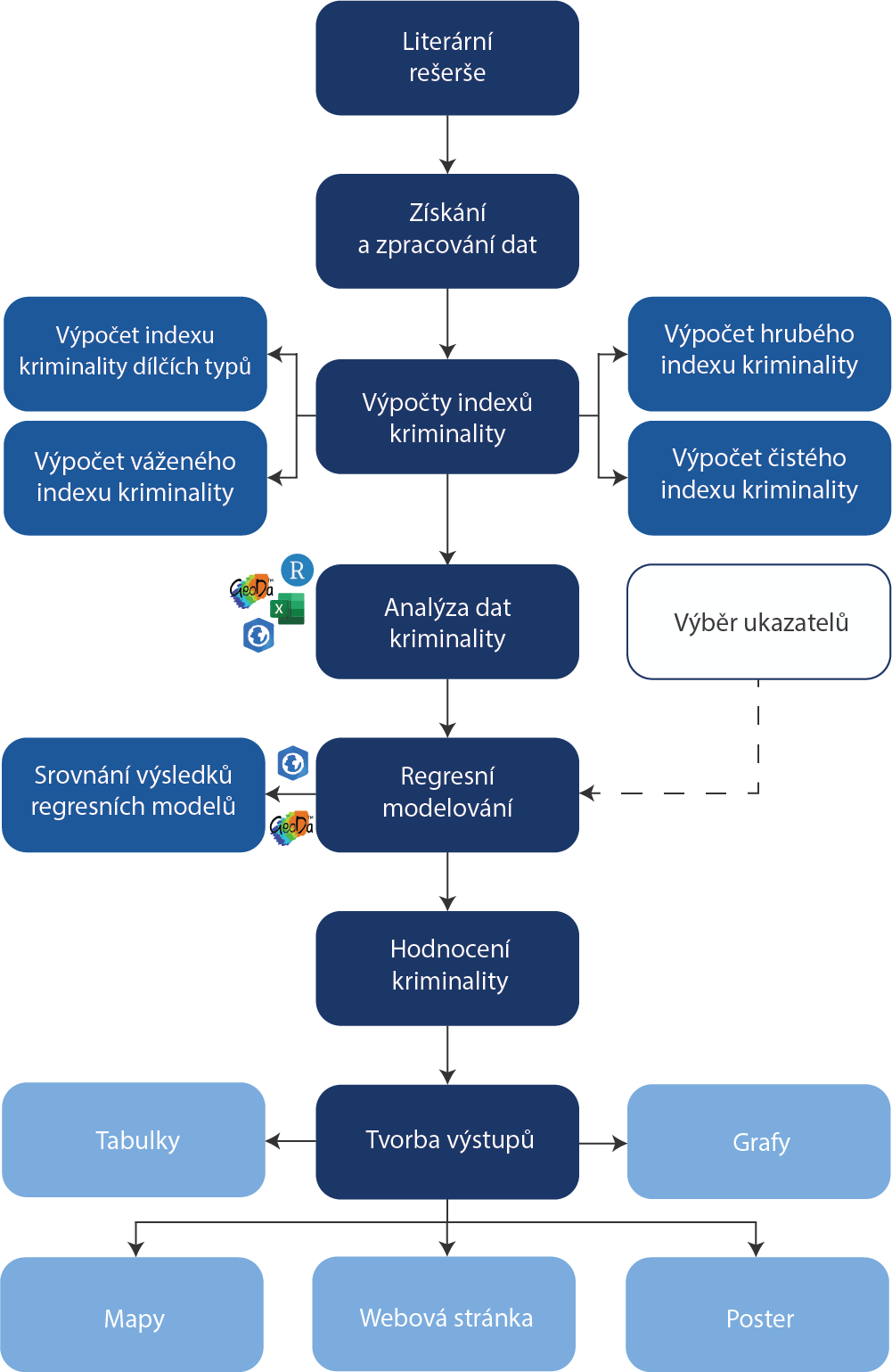
Regresní analýza
Regresní modelování má za cíl analyzovat vztah mezi vysvětlovanou závislou (vysvětlovanou) proměnnou a jednou nebo více nezávislými (vysvětlujícími) proměnnými (prediktory). Tento postup umožňuje odhadnout vliv prediktorů na sledovanou proměnnou. Lineární regresní model je nejjednodušší formou regresní analýzy, kdy je vztah mezi proměnnými aproximován lineární funkcí (tj. přímkou, která nejlépe popisuje datovou sadu). Geometricky se tak jedná o úsečku, která nejlépe prochází množinou bodů v rovině. Vztah je definován následující rovnicí:
𝒚 = β 0 + β 1 + ε
,kde 𝒚 je sledovaná proměnná, β0 je úrovňová konstanta, β1 regresní koeficient proměnné x a ε je vektor náhodné chyby měření.
Prostorové regresní metody rozšiřují klasické regresní modely tím, že zohledňují prostorovou strukturu dat, která často vykazuje nedostatek nezávislosti mezi měřeními provedenými na blízkých místech. Existuje několik různých přístupů k prostorovým regresním analýzám. Obvykle se využívají dva základní přístupy: globální řešení pomocí explicitní formy prostorovéautokorelace pro zohlednění celkového vlivu prostorové závislosti a místní řešení umožňující modelování prostorově proměnných parametrů (tj. GWR) na místní úrovni. Globální řešení přímo hodnotí prostorovou složku dat (často jako nezávislou proměnnou) a zahrnuje ji do návrhu modelu. Čistý prostorový autoregresní model se týká autoregrese závislé proměnné, avšak je nutno upozornit na společné autoregresní rysy i v jiných modelech, včetně prostorového chybového modelu. Existuje jednotný koncept globálních modelů prostorové závislosti, který vysvětluje vazby mezi těmito modely. Prostorový lag model, angl. Spatial Lag Model (SLM), neboli smíšený regresní prostorový autoregresní model zahrnuje složky standardního regresního modelu X𝛽 (kde X je vektor nezávislých proměnných a 𝛽 jsou regresní koeficienty) a také prostorově zpožděnou verzi závislé proměnné 𝒚 (následující rovnice) s vektorem prostorových autoregresních parametrů ρ, váhovou maticí W a vektorem chyb ε.
𝒚 = Xβ + ρWy + ε
Prostorový chybový model, angl. Spatial ErrorModel (SEM) je definován následující rovnicí, která zahrnuje prostorové autoregresní parametry λ pro chyby a vektor jednotkových chyb. Prostorová autokorelace se nezahrnuje do modelu jako samostatná proměnná, ale ovlivňuje kovarianční strukturu náhodných chybových členů.
𝒚 = Xβ + ε; ε = λWε + u
Prostorový chybový model je volen tehdy, pokud se zdá, že existuje statisticky významná prostorová autokorelace, avšak testy prostorových zpožděných efektů neposkytují dostatečné důkazy pro zahrnutí těchto efektů. Model prostorového zpoždění je vhodnější v situacích, kdy nepozorované proměnné nemají statisticky významný vliv, zatímco model prostorové chyby je upřednostňován, pokud jsou nepozorované proměnné relevantní. Nicméně, tyto modely jsou kritizovány za svůj univerzální přístup.
Metoda OLS (Ordinary Least squares)
OLS umožňuje vyhodnotit celkovou výkonnost modelu a poukázat na vliv prostorové složky (heteroskedasticita, nestacionarita, prostorová autokorelace reziduí, aj.). Dále umožňuje identifikovat prediktory s globální multikolinearitou. Pro vyhodnocení globální multikolinearity se často používá Variance Inflation Factor neboli faktor zvětšení rozptylu (VIF). Tento ukazatel udává, nakolik je rozptyl odhadovaných regresních koeficientů zvětšen ve srovnání se situací, kdy by prediktory byly vzájemně nezávislé. Prediktory s hodnotami VIF větší než 5, 7,5 či 10 by podle odborníků měly být eliminovány z důvodu vážné multikolinearity. Je však třeba si uvědomit, že interpretace VIF by neměla být prováděna izolovaně, ale v kontextu (např. s ohledem na statistickou významnost prediktorů). Existují další faktory, které mohou ovlivnit stabilitu regresních koeficientů, včetně velikosti vzorku, podílu rozptylu závislé proměnné spojeného s nezávislými proměnnými a rozptylu nezávislé proměnné. Tyto faktory mohou buď zmírnit nebo zhoršit účinky multikolinearity.
Metoda geograficky vážené regrese (GWR)
Metoda GWR umožňuje prostorovou variabilitu koeficientů β. Koeficienty β(t) jsou vyhodnocovány pro každý cílový bod (tj. centroid polygonu) pomocí prostorově vážené regrese metodou nejmenších čtverců na množinu bodů v poloměru r. Místo fixní hodnoty pro r je použita funkce distance-decay f(d) – Gaussova, bilineární nebo kubická. Optimalizace výsledků je dosažena úpravou šířky pásma, která se často provádí experimentálně na základě minimalizace hodnoty Akaikeho informačního kritéria (Akaike Information Criterion – AIC). Metoda GWR tedy rozšiřuje tradiční regresní rámec o pohyblivé regresní parametry, které umožňují odhadovat jejich lokální podobu. Tato metoda umožňuje aplikaci obecného regresního modelu na prostorově proměnná data, kde lze předpokládat prostorovou variabilitu regresních parametrů. GWR tak nabízí nový přístup k modelování prostorových dat, který umožňuje lépe zachytit lokálně specifické (prostorové) vzorce a vztahy. Matematický zápis modelu GWR lze charakterizovat vztahem:
𝒚 = 𝑿𝜷(𝒕) + 𝜺
Použitá data
V této práci je použito několik následujících metod a přístupů. Program Marxan k výpočtům řešení využívá metodu simulated annealing. Hodnocení stavu degradace biodiverzity probíhá na základě výpočtů hnacích sil průměrného zastoupení druhů. Byl také použit integrovaný přístup obou modelů a testování míry integrace.
Pro účely geostatistické analýzy byla nutná akvizice požadovaných dat za sledované období pro specifické charakteristiky, která odpovídají požadavkům prostorového modelování a jsou v rámci možností dostatečně kvalitní a prostorově detailní. Diplomová práce vzhledem ke komplexnímu zaměření, které propojuje strukturu zjištěné trestné činnosti s vysvětlujícími charakteristikami, využívá dva základní typy datových zdrojů,
a sice data o trestné činnosti za období 2012 až 2021 a socioekonomická data
za obyvatelstvo v roce 2021. Hlavním zdrojem poskytující informace o demografické
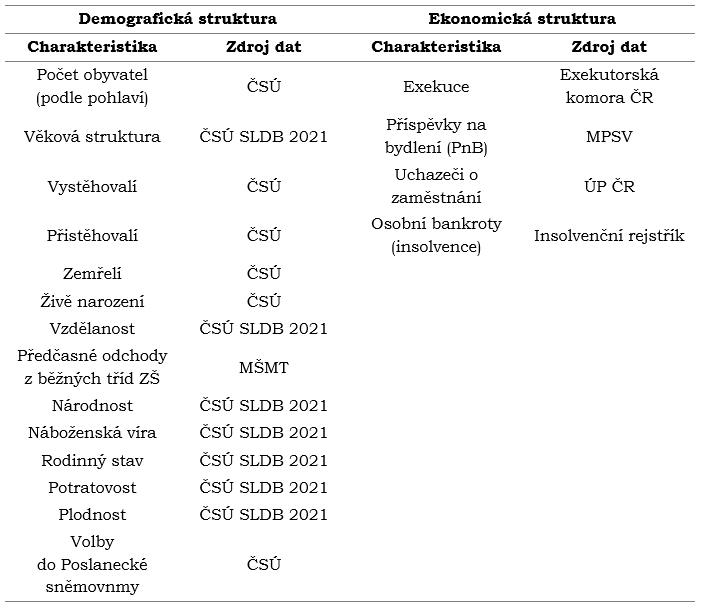
a socioekonomické struktuře je Český statistický úřad (ČSÚ), který poskytuje mj. data pocházející ze Sčítání lidu, domů a bytů v roce 2021 (SLDB 2021). Získaná socioekonomická statistická data svou kvalitou, kvantitou a také prostorovou podrobností zcela vyhovují požadavkům pro jejich využití v geostatistických analýzách. Kromě ČSÚ posloužily zdroje dat poskytnuté Exekutorskou komorou ČR, Ministerstvem školství, mládeže a tělovýchovy České republiky (MŠMT ČR), Úřadem práce České republiky (ÚP ČR) a Ministerstvem práce a sociálních věcí České republiky MPSV ČR. Seznam vybraných socioekonomických dat je patrný z následující tabulky:
 V České republice existují dva oficiální registry exekucí, konkrétně Centrální evidence exekucí, kterou spravuje Exekutorská komora České republiky, a Rejstřík zahájených exekucí, který je spravován Ministerstvem spravedlnosti. Oba tyto registry však nezahrnují exekuce správní a daňové povahy, což způsobuje, že v České republice chybí podstatné informace o celkovém počtu probíhajících exekučních řízení.
Prostorová data o kriminalitě pochází z evidence spáchané trestné činnosti Policie České republiky, která jsou dostupná prostřednictvím portálu na adrese Mapa kriminality.
Pro analytické účely byly za prostorovou administrativní jednotku vybrány obce ze čtyř následujících důvodů:
V České republice existují dva oficiální registry exekucí, konkrétně Centrální evidence exekucí, kterou spravuje Exekutorská komora České republiky, a Rejstřík zahájených exekucí, který je spravován Ministerstvem spravedlnosti. Oba tyto registry však nezahrnují exekuce správní a daňové povahy, což způsobuje, že v České republice chybí podstatné informace o celkovém počtu probíhajících exekučních řízení.
Prostorová data o kriminalitě pochází z evidence spáchané trestné činnosti Policie České republiky, která jsou dostupná prostřednictvím portálu na adrese Mapa kriminality.
Pro analytické účely byly za prostorovou administrativní jednotku vybrány obce ze čtyř následujících důvodů:
1.) prostorové analýzy v poměrně podrobném prostorovém měřítku
2.) dostatečné množství statistických charakteristik a záznamů
3.) dostupnost a aktuálnost dat
4.) obce jsou lukrativním kompromisem mezi detailností geoanalýzy a zachováním anonymity jednotlivých případů trestných činností.
Použití prostorových polygonových dat administrativního členění (obce, SO ORP, kraje, stát) vychází z otevřené datové sady RÚIAN (Registru územní identifikace, adres
a nemovitostí). Data RÚIAN jsou vytvářena každý den (pokud došlo v některém prvku obce ke změně). Předpřipravené soubory jsou generovány jednou měsíčně a jsou k dispozici ve formátu Shapefile vyvinutou firmou Environmental Systems Research Institute (Esri) v souřadnicovém systému jednotné trigonometrické sítě katastrální (S-JTSK). V práci byla použita data RÚIAN, jež přísluší k datu 4. 2. 2022
a odpovídají prostorovému měřítku 1 : 5 000. Data poskytuje Český úřad zeměměřický
a katastrální.