Diplomová práce

Prvním z významných výstupů práce je hodnocení míry kriminality prostřednictvím výpočtů (souhrnného) čistého a hrubého indexu kriminality v Česku za období 2016–2021. Jednotlivé mapy jsou součástí příloh 1–12. Vizualizací pomocí animace lze zachytit dynamiku vývoje míry kriminality ve sledovaném období (přílohy 71 a 72). Výpočet indexů byl realizován užitím geografického informačního systému (GIS) ArcGIS Pro. Autor práce se inovativně zaměřil na využití dat trestných činů z webové aplikace Mapy Kriminality. V rámci testování této datové sady bylo zjištěno, že data v letech 2012–2015 pravděpodobně neobsahují kompletní informace evidovaných trestných činů, a proto byla z analýz vyloučena. Některé typy trestných činů nemohou být s ohledem na interní pravidla Policie ČR veřejnosti poskytnuta.Snahou bylo zachytit prostorovou koncentraci míry kriminality v maximálně nejpodrobnějším detailu. Tato práce reflektuje potřebu výzkumu kriminality v detailním prostředí, a sice na úrovni obcí, což činí tuto práci v českém kontextu výjimečnou a dosud unikátní i z hlediska použitých metod a datové sady. Na základě výsledných map vypočteného souhrnného indexu kriminality za dílčí roky sledovaného období lze konstatovat, že kriminalita je nejvíce koncentrována v Praze, na Mostecku, Ostravsku, velkých městech s vysokým počtem obyvatel, a poté v některých místech při pohraničí (s výjimkou JV Česka). Dalšími důležitými výstupy jsou mapy indexů míry kriminality dílčích kategorií trestných činů za jednotlivé roky 2016–2021. Matice map je obsažena v příloze 24 a animace jsou k dispozici v přílohách 13–23. Souhrnné statistiky dílčích kategorií trestných činů jsou obsaženy v příloze 73. Bližší interpretace výsledků analýzy časového vývoje typů trestných činů je součástí podkapitoly 4.1.3. Změny v trestní politice, tj. zákonodárné změny v oblasti trestních zákonů a předpisů na ně navazujících nebyly brány v úvahu během analýzy kriminality.

Dílčí částí výsledků práce je autorem navržený jedinečný a inovativní postup výpočtu váženého indexu kriminality (viz podkapitola 4.1.2). Autor navrhl a následně realizoval výpočet váženého indexu kriminality pro rok 2021 v obvodních odděleních Česka. K tomu byla využita data Policie ČR všech registrovaných typů trestných činů dle takticko-statistické klasifikace (TSK). Ve výpočtu jsou zahrnuty váhy, které byly vypočítány na základě průměrné délky trestu nepodmíněného odnětí svobody (v měsících) pro každý typ trestné činnosti klasifikovaných podle trestního zákona (TZ). Dané hodnoty vah byly následně vynásobeny počtem příslušných trestných činů (klasifikovaných podle TSK, kde je současně obsažen i příslušný paragraf skutku v TZ), vyděleny počtem trestně právních obyvatel (ve věku 15 let a více) a vynásobeny hodnotou 10 000. Dílčím výsledkem práce je pokročilá vizualizace váženého a čistého indexu kriminality v obvodních odděleních užitím metody Bivariate colors (následující orbázek). Z mapy je patrné, že kriminalitou jsou nejvíce zatíženy Praha, Mostecký okres, Jindřichohradecký okres, Českolipský okres, Bruntálský okres, Ostrava a další velkoměsta s počtem obyvatel přesahujícím 150 tisíc. Naopak nejnižší hodnoty indexu kriminality jsou zaznamenány na pohraničí se Slovenskem, ve východní části Vysočiny, v Pardubickém kraji až po střední oblast Karlovarského kraje. Charakteristika dosažených výsledků prostorové koncentrace míry kriminality potvrzuje skutečnost, že kriminalita není v geografickém prostoru distribuována náhodně.

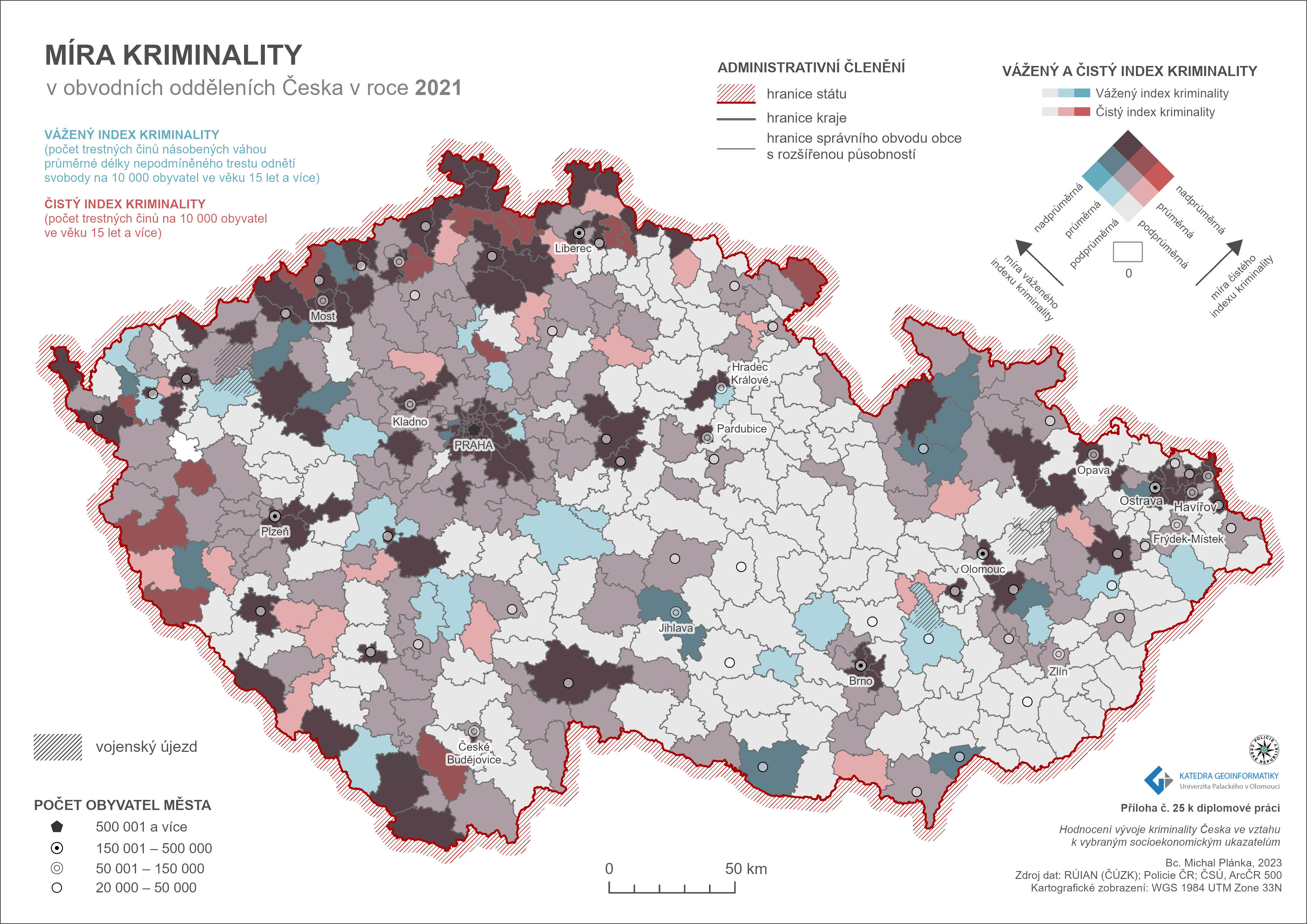
Další signifikantní část výsledků představuje nalezení vztahů mezi kriminalitou a socioekonomickými ukazateli na úrovni obcí v roce 2021, čehož bylo docíleno užitím regresního modelování ve spolupráci s GIS ArcGIS Pro a GeoDa. Bylo zjištěno, že hodnoty indexu kriminality nevykazují normální rozdělení. S ohledem na velké množství obcí (1 010) vykazující nulovou hodnotu indexu kriminality bylo regresní modelování realizováno pro dva scénáře, označené jako MODEL 1 a MODEL 2. V MODELU 1 je pracováno s předpokladem, že všechny existující hodnoty jsou s jistou mírou spolehlivosti správné, tzn. existující odlehlé hodnoty nevznikly chybou měření nebo záznamu, ale popisují skutečný stav kriminality v 6 254 obcích (bez vojenských újezdů). Oproti tomu v MODELU 2 došlo k eliminaci obcí (5 244) s nulovým indexem kriminality. Logaritmizace dat zajistila v indexu kriminality pozitivní změnu normality v případě MODELU 2.

Před hlavní analytickou částí tvořenou aplikací neprostorové metody Ordinary least squares (OLS) byl proveden výběr demografických (19) a ekonomických (4) ukazatelů na základě předešlých tuzemských i zahraničních vědeckých výzkumů, dostupnosti, podrobnosti a časové aktuálnosti a podle autorova vlastního uvážení po konzultaci s odborníky. Poté byla provedena základní exploratorní analýza vstupní datové sady. Cílem tohoto kroku bylo odhalit a shrnout statistické charakteristiky použité datové sady, což zahrnuje rozložení hodnot jednotlivých ukazatelů, identifikaci odlehlých hodnot a vyhodnocení vztahů mezi indikátory. Vzhledem k tomu, že většina ukazatelů není charakterizována normálním rozdělením dat, byl pro všechny kombinace ukazatelů obou scénářů vypočten Spearmanův korelační koeficient (přílohy 49 a 50). Podrobné výsledky OLS poskytují reporty z programu ArcGIS Pro pro MODEL 1 (příloha 59) a pro MODEL 2 (příloha 60). Obsah reportů z programu GeoDa je pro MODEL 1 obsažen v příloze 68 a pro MODEL 2 v příloze 69. Hodnota koeficientu determinace (R²) regresních modelů je relativně velmi nízká. Pro MODEL 1 se pohybují kolem hodnoty 0,17, což naznačuje, že změny hodnot chyb nelze vysvětlit pomocí hodnot zkoumaných parametrů z více než 17 %. V případě použití MODELU 2 je možno vysvětlit téměř 15 % rozptylu závislé proměnné.

Následně došlo k sestavení několika regresních modelů pro oba scénáře, kde byly postupně odstraněny ukazatelé prokazující vysokou multikolinearitu, aby bylo dosaženo co nejpřesnějších výsledků. Finální model byl optimalizován pomocí stepwise regrese. Při diagnostice modelu bylo odhaleno narušení některých předpokladů regresního modelování, a to především přítomností heteroskedasticity a prostorové autokorelace reziduí. Ta poukazuje na prostorovou heterogenitu a nestacionaritu, což má za následek nevhodnost aplikace klasických statistických metod. Užitím OLS bylo zjištěno, že s rostoucím podílem obyvatel náboženského vyznání roste také index kriminality. Z hlediska rodinného model odhalil situaci, že s rostoucím počtem svobodných a rozvedených roste i míra kriminality. Dle modelu platí, že s rostoucím podílem obyvatel v insolvenci klesá index kriminality. OLS vyhodnotil, že s rostoucími hodnotami indexu kriminality roste podíl obyvatel v exekuci, romské populace a příjemců PnB. Výsledkům OLS je podrobněji věnována pozornost v podkapitole 4.3.1. Zajímavým dílčím výsledkem práce je prostorová vizualizace vybraných dílčích socioekonomických ukazatelů v podobě map (přílohy 26 až 48).

Poté byly aplikovány a porovnány modely Spatial lag model (SLM) a Spatial error model (SEM), avšak žádný z nich nebyl vybrán z důvodu nenaplnění předpokladů výrazného zlepšení v kontextu R² a Akaike informačního kritéria (AIC). Výsledné modely stále bohužel vykazují heteroskedasticitu, kterou prostorové modely nedokázaly eliminovat. Srovnání regresních koeficientů OLS, SLM a SEM pro oba scénáře shrnuje příloha 75.

Aplikace lokální prostorové metody Geographically weighted regression (GWR) pro oba scénáře přináší efektivnější, kvalitnější a přesnější výsledky regresních koeficientů ve srovnání s metodami SLM, SEM či neprostorovou metodou OLS. Pro srovnání bylo využito několik statistik, mezi které náleží hodnota koeficientu determinace R² a AIC. V tomto případě platí, že vyšší explanační sílu modelu GWR před modely OLS, SEM a SLM indikuje nižší hodnota AIC (MODEL 1 – 75 687; MODEL 2 – 1 774). Metoda GWR posloužila ke hledání vztahů mezi indexem kriminality a osmi prediktory – index stáří, podíl obyv. bez vzdělání, podíl obyv. v exekuci, podíl obyv. v insolvenci, podíl obyv. s náboženským vyznáním, podíl svobodných, podíl rozvedených, volební účast). Regresní koeficienty byly vizualizovány prostřednictvím map (obr. 12 až 19). Interpretace výsledků regresních koeficientů GWR je zaměřena především na statisticky významné oblasti MODELU 1, viz podkapitola 4.3.3.