Chí kvadrát testy

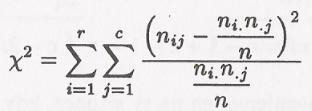
Testy normality

Celá řada statistických hypotéz je založena na faktu, že je předem známé pravděpodobnostní rozložení dat. Testy normality sledují, zda datový soubor pochází z normálního rozdělení. Testy normality lze řešit početně i graficky.

Grafická vizualizace testů normality

Principem grafických vizualizací testů normality je uspořádání dat a následně jejich porovnání s normálním rozdělením. existuje několik možností grafických vizualizací normality.

Histogram
Box plot
QQ plot (Quantile-quantile plot)
PP plot (Probability-probability plot)
NP plot (Normal probability plot)

Chí kvadrát test dobré shody

Chí kvadrát test umožňuje zjistit, zda má sledovaný jev opravdu předem známe rozdělení dat. Tato metoda vychází z porovnání skutečného rozdělení dat s teoretickým zvoleným rozdělením, které bylo určeno na základě úvah, předchozích zkušeností či pomocí grafické vizualizace. Shodu těchto četností je nutné ověřit Chí kvadrát testem dobré shody.

Testy dobré shody se liší poze podle toho, zda jsou známy parametry μ a σ². Testová statistika je určená matematickým vztahem , kde Xi jsou pozorované četnosti a npi jsou teoretické četnosti. Kritický obor je omezen hodnotou χ² (1-α) při k-1 stupních volnosti. Pokud hodnota χ² přesáhne tento kritický obor, pak řekneme, že data nepocházejí z normálního rozdělení. Testová statistika je podobná pro případ testu se známými i neznámými parametry. Liší se pouze ve snížení stupňů volnosti o počet neznámých parametrů v případě Chí kvadrát testů o neznámých parametrech.

Z dalších testů normalit mohou být jmenovány například Shapiro-Wilkův test, případně Wilkoxonův párový test.

Testy nezávislosti

Tsty nezávislosti jsou nečastější používanou formou χ² testů. Jsou využívány hlavně pro kontingenční tabulky. Testy nezávislosti jsou založeny na testech o neznámých parametrech a jejich úkolem je zjístit, zda jsou na sobě jevy závislé či nikoliv.

Testová statistika je dána matematickým vztahem při χ² rozdělení o (r-1)(s-1) stupních volnosti. Pokud je hodnota Χ² vyšší než hodnota testového kritéria, zamítáme hypotézu o nezávislosti.

Konkrétními χ² testy nezávislosti mohou být McNemarův test pro kontingenční tabulky, Kruskal-Wallisův test či Lillieforsův test.

Dostupnost testů v různých softwarech

Veškeré statistické výpočty a vizualizace lze provést v softwaru R-project a většinu z nich také v softwaru Microsoft Excel. V softwaru ArcMap je možné vytvořit grafické vizualizace normality, jako jsou histogram a QQ plot, stejně jako vypočítat relativní četnosti a vytvořit pro ně graf. Další možností je software IDRISI, které ve verzi Taiga umí taktéž vypočítat relativní četnosti a zvizualizovat je. Dále tento software nabízí možnost tvorby kontingenčních tabulek a histogramů.