Stanovení minimální absolutní chyby
Kvantifikace odchylek (zkráceno)
Pro stanovení absolutní chyby metody byla použita pořadová klasifikace metod – nikoli kvantitativní. Výhodou je snadné provedení, omezení spočívá v tom, že pro novou sadu metod (povrchů) musí být provedena znovu, protože nemá obecný charakter, pouze komparativní. Takže ve výsledku lze očekávat tvrzení, že jedna metoda je lepší či horší než druhá.
Na vyšší úrovni by bylo stanovení obecného kvantitativního ocenění povrchů, resp. jejich zvolených charakteristik. Výsledná hodnota pro ten který povrch by se počítala podle přesně stanoveného vzorce, který by se mohl použít kdykoli a opakovaně. Problémem u takového stanovení potom je výběr správných charakteristik. Ty musejí být relevantní a hlavně na sobě nezávislé.
Analýza přesnosti DMR by se měla skládat z identifikace chyb, jejich kvantifikace a následného odstranění. K identifikaci se využívají buď statistické metody nebo různá vizualizace povrchu. Počínaje barevnou hypsometrií, přes deriváty původního DMR (sklon, orientace, křivost, stínovaný reliéf), vykreslení vrstevnic a konče 3D zobrazením. Ke kvantifikaci se za moment dostaneme… Odstranění identifikovaných chyb se věnovali např. Mitášová, Mitáš (1993).
Dobrou charakteristikou vedoucí ke kvantifikaci chyb je tzv. Hammock plot. Grid nadmořských výšek je zaokrouhlen na celá čísla a je provedena analýza zbytků po dělení celým číslem, které typicky představuje interval původních vrstevnic (ne nutně musejí data pocházet z vrstevnicového modelu). Podle tohoto intervalu jsou pixely rozřazeny do tolika kategorií, kolik byl zmíněný interval. Jedná se tak vlastně o barevnou hypsometrii po jednom metru s opakující se barevnou škálou. Takto vykreslený povrch daleko lépe vystihuje detailní rysy reliéfu než klasická barevná hypsometrie, která trpí velikostí jednoho barevného stupně. Lze pak např. vidět markantní rozdíl mezi přiřazováním hodnot metodou IDW a Spline.
Mnohem obtížnější je z Hammock plotu vyvodit relevantní numerickou charakteristiku. Existuje tzv. Hammock index (Wood, 1996):
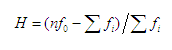n … celočíselný dělitel
f0 … četnost Mod(0) (pixelů se zbytkem nula)
fi … četnost zbylých Mod.
Tento index vyjadřuje podíl pixelů se zbytkem nula na celkovém množství pixelů. Vůbec ale právě nebere ohled na četnost pixelů uvnitř zbylých Mod(x). Teoreticky by rozložení ve všech kategoriích Hammock plotu mělo být vyrovnané a Hammock index by pak měl ideální hodnotu rovnou 1/(n – 1). Hodnota indexu je –1, pokud mod(0)=0 px; je (n – 1), pokud mod(0)=(1/2 všech pixelů). Hodnota se blíží nekonečnu, pokud roste podíl pixelů v mod(0).
Některé charakteristiky byly vyřazeny, protože jejich informaci už poskytuje jiná charakteristika (např. vyřazení analýzy četností nadmořských výšek ve prospěch hodnocení diferenčních povrchů). Nakonec bylo vybráno šest statistických charakteristik:
1. mean difgrd-abs [m] – průměrná absolutní odchylka průměrového gridu od referenčního povrchu;
2. Q75 difgrd-abs [m] – kvantil absolutních odchylek na úrovni 75 %, odstraňuje vliv extrémních hodnot;
3. max difgrd-abs [m] – maximální absolutní odchylka od referenčního povrchu;
4. R difgrd [m] – variační rozpětí gridu odchylek, tj. rozdíl maximální a minimální hodnoty;
5. T-test grdref vs. grdmean – testuje hypotézu o rovnosti středních hodnot obou povrchů;
6. F-test grdref vs. grdmean – testuje hypotézu o rovnosti rozptylů obou povrchů.
Ideální situací je, když jsou první čtyři charakteristiky minimální a oba testy nezamítnou shodu. Každé charakteristice navíc byla stanovena váha – ve stejném pořadí takto: 0,25 – 0,25 – 0,20 – 0,20 – 0,05 – 0,05.
Příloha 11 obsahuje statistické charakteristiky – kromě výše uvedených jsou pro přehled vypsány i hodnoty jako outliers: procento pixelů hodnotou ležících mimo interval definovaný tzv. whisker-y, které jsou vzdáleny 1,5•IQR od kvartilů (IQR … interquartile range). Outliers jsou extrémní hodnoty datového souboru – čím méně jich je, tím lépe. Dobrou srovnávací informaci však podají pouze tehdy, pokud dva datové soubory dosahují přibližně stejného IQR. Nejnižšího procenta mimoležících bodů totiž dosahuje právě Trend, a to díky vysokému IQR. Dále jsou uvedeny charakteristiky Rd a Rq, což je decilové a kvartilové rozpětí, nebo špičatost a šikmost kolem střední hodnoty. U výsledku testů je vepsáno ano (ne), pokud nebyla (byla) zamítnuta hypotéza o shodnosti.
V Příloze 12 jsou pak vybrané statistiky přepsány do pořadí od nejlepší (1) po nejhorší. Váženou kombinací je pak odvozen celkový výsledek metody, načež je sestaveno konečné pořadí metod pro dané území.
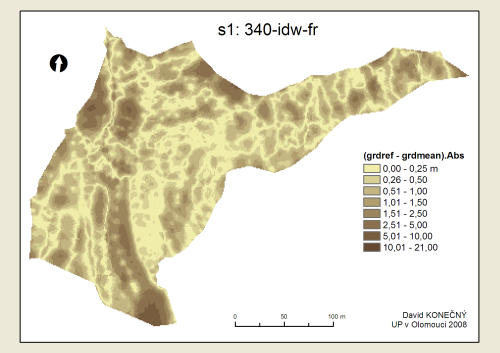
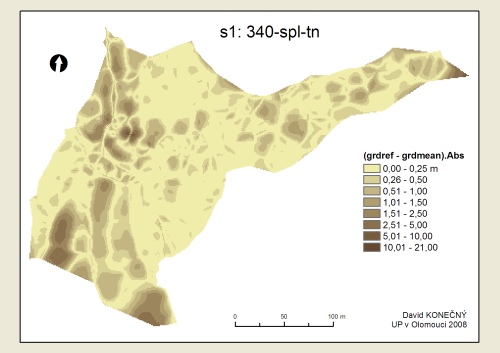
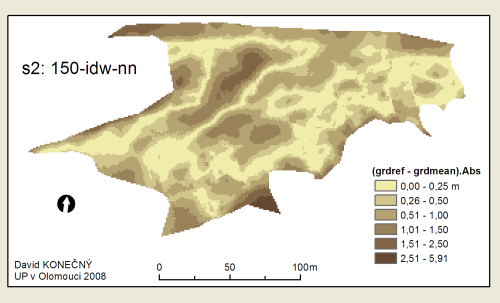
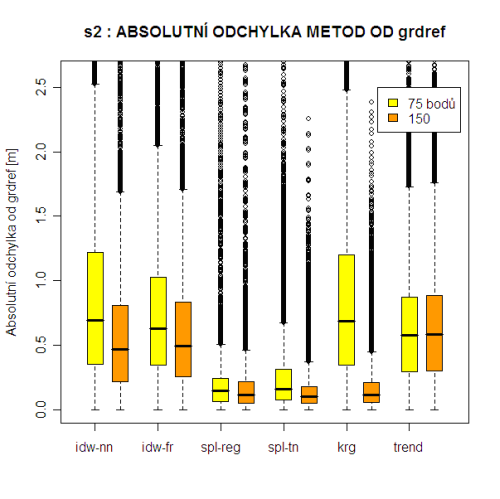
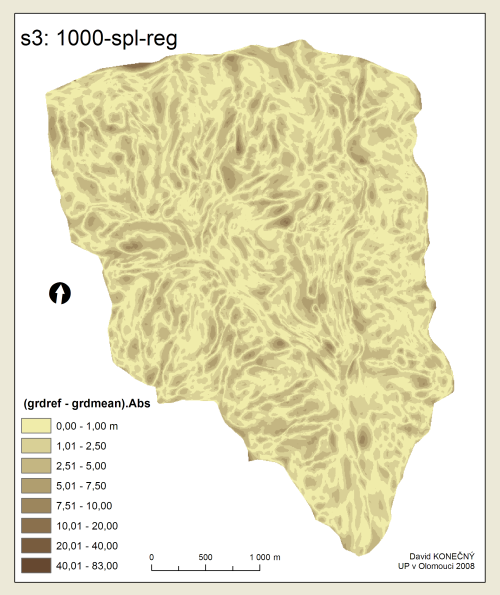
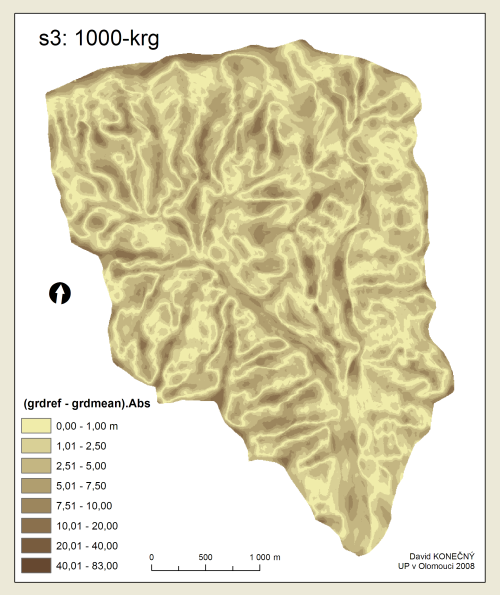
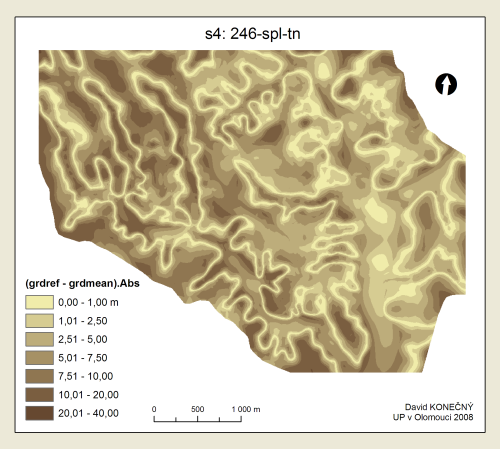
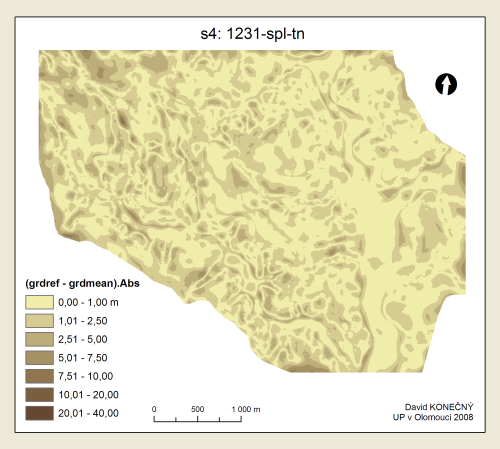
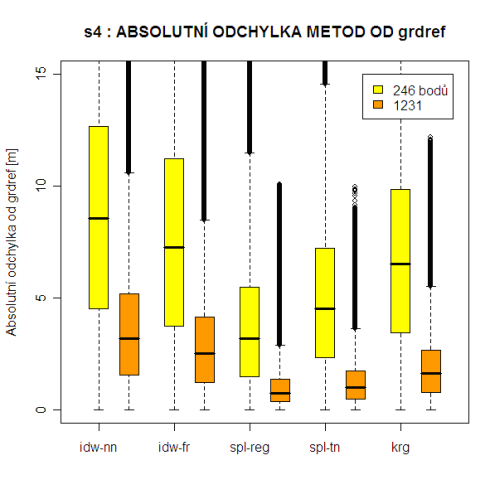
Přehled pořadí přesnosti metod, což je vlastně hlavním výsledkem této práce, je uveden v tabulce Tab. 3. K tomu byly ještě sestaveny tzv. boxploty (neboli box-and-whisker diagramy) gridů absolutních odchylek od referenčního povrchu (viz Příloha 13–21), které podávají grafický přehled rozložení hodnot v jednotlivých gridech. Grafická podoba povrchů difgrd-abs je obsahem Příloh 1–5. Pro srovnávání je však lepší použít digitální přílohy na DVD.
Tab. 3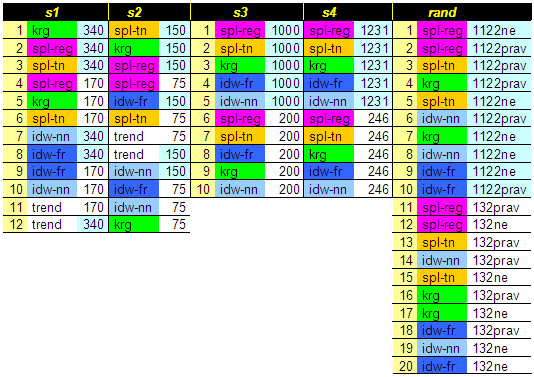
Z tabulky Tab. 3 lze vysledovat, že podle očekávání vyšší hustota vstupních bodů podmiňuje přesnější interpolaci. Pro území rand, s3 a s4 se všechny aplikace metod na větší počet bodů umístily lépe než aplikace na menší počet vstupů. U sesuvných území s1 a s2 tomu tak nebylo, nicméně až na metodu Trend vždy dosahovala lepšího výsledku konkrétní metody ta, která použila více bodů. U Trendu tomu bylo vždy naopak – metoda si lépe vedla s menším počtem bodů. Podle 2. části Přílohy 11 je však zřejmé, že rozdílná hustota bodů na výsledek neměla až tak velký vliv – oba povrchy v rámci jednoho území jsou si velice podobné. Vždyť jejich vzájemná průměrná absolutní odchylka je 14 cm pro s1, resp. 4,4 cm pro s2, což je v porovnání s odchylkou od referenčního povrchu (4 m, resp. 63 cm) opravdu málo.
U území s2 malý počet vstupních bodů neblaze ovlivnil výsledek jinak relativně přesné metody Kriging. I na ostatních územích vyjma s1 lze pozorovat, že Kriging je náchylný na dostatečný počet vstupních bodů a v aplikacích na menší hustotu bodů se řadí mezi horší metody, i když jinak podává dobré výsledky.
Na území rand je u všech metod až zázračně dodržen poměr zhruba 3× menší průměrná absolutní chyba u větších výběrů než u menších, a to u pravidelného i nepravidelného rozmístění bodů. Nabízí se paralela se strukturou výběru bodů 3×3, resp. 9×9. Tato závislost je v menší míře pozorovatelná i u charakteristik kvantilových rozpětí (difgrd) či u Q75 a max (difgrd-abs). Podobnou paušální závislost u ostatních území nelze pozorovat.
Obecně lze z výsledků vyvodit, že největší přesnosti dosahuje regularizovaný Spline těsně následovaný metodou Spline s tenzí. Někde uprostřed se umístil Kriging. S lehkým odstupem pak obě metody IDW, přičemž IDW Fixed Radius dosahuje mírně lepších výsledků než IDW Nearest Neighbors.
U území s3 a s4 se toto pořadí jasně ukazuje kromě toho, že metoda IDW FR na menší hustotě bodů v území s3 „přeskočila“ Kriging. Jinak takto idealizované pořadí samozřejmě není dodrženo na všech územích. Na sesuvných územích s1, s2 dosahuje výborných výsledků Kriging (na vyšší hustotě bodů). Na imaginárním území si oproti pořadí dobře vedla metoda IDW NN na 132 pravidelně rozmístěných bodech, naopak u IDW FR 1122prav je na boxplotu v Příloze 13b vidět velké vychýlení oproti přesnosti všech ostatních metod.
Co se týče pravidelnosti či nepravidelnosti rozmístění vstupních bodů, tak v případě metod aplikovaných na menší počet bodů platí, že pravidelnost dosahuje celkově menších odchylek. To platí i pro větší hustotu bodů vyjma metod regularizovaný Spline (těsně) a IDW FR. Rozdíly mezi charakteristikami dvojic povrchů jsou však opravdu minimální, zvláště u regularizovaného Splinu, takže relevantní důkaz o vhodnosti toho či onoho rozmístění bodů pro interpolaci nelze podat.
Autor si je vědom toho, že takto sestavené pořadí metod je získáno na podkladě pouhých pěti konkrétních území, a tím pádem nemusí platit obecně. Kadlčíková a Tuček (2008) uzavřeli svůj projekt vyzdvižením metody Spline s tenzí jako nejvhodnější metody pro interpolaci na testovaných typech reliéfu v ČR. Tato práce v závěru doporučuje metodu jinou. Je však stále více jasné, že schopnost metody Spline (obecně) vytvářet hladké povrchy je pro modelování reliéfu v České republice ta pravá, která ji staví do popředí. Je však třeba mít na paměti, že stále existuje nejistota, zda toto tvrzení lze zobecňovat. Existují typy reliéfu, jež mohou vykazovat znaky, které nebudou slučitelné s hladkostí povrchu. Pak zcela jistě budeme nuceni hledat jinou metodu.
Typ reliéfu je tedy hlavním činitelem pro výběr konkrétní metody interpolace, a proto operátor konstruující digitální výškový model musí své území znát nebo alespoň musí mít takové podklady, které mu reálný povrch přiblíží.
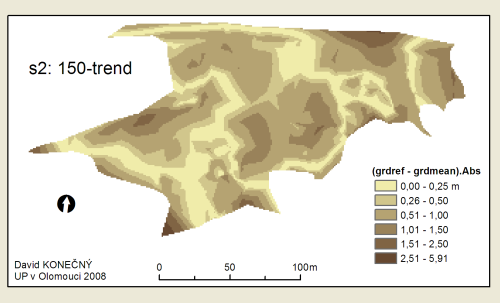
Ilustrovat to může např. výsledek metody Trend na území s2. Jedná se o malé území, které není příliš „zvlněné“ – je to část svahu, takže zde nenajdeme vyloženě vrcholy či údolí. Potom i Trend zde může být vhodná metoda interpolace výškových dat.
Vydedukovali jsme, že reliéf v Česku má ponejvíce hladký průběh, a je proto vhodné jej modelovat pomocí metod založených na křivkách Spline. Bylo také zjištěno, že IDW nedosahuje až takové přesnosti. Pro budoucnost metody IDW v oblasti interpolace povrchů by bylo vhodné najít takové nastavení parametrů, které bude generovat přesnější povrchy – tj. např. snížit hodnotu power nebo zakomponovat nějaký vyhlazovací faktor.
Pro ilustraci je zde uvedeno jen pár grafických výstupů…
